
In thermal ionisation mass spectrometry it is common practice, to correct (dynamic) mass discriminations, which are caused by the progressing evaporation of the sample from the evaporation filament, by the application of one of the so-called "fractionation laws" .
Very often, however, such evaporation induced biases are overlain by static biases of may be very different origin:
A classic static discrimination, as e.g. known from Multicollector (MC) IRMS, is caused by so-called (oftenly drifting) channel gain factors. They have been a major obstacle in the early years of MC technology , before manufacturers have finally learnt to produce virtually offset-free Faraday cups.
Another well known static discrimination ( in radial and/or axial direction) is arising during transit of the ion beam through the ion optical system, where parts of the ion beam may be cut-off at beam-defining stops.
Very often, however, such evaporation induced biases are overlain by static biases of may be very different origin:
A classic static discrimination, as e.g. known from Multicollector (MC) IRMS, is caused by so-called (oftenly drifting) channel gain factors. They have been a major obstacle in the early years of MC technology , before manufacturers have finally learnt to produce virtually offset-free Faraday cups.
Another well known static discrimination ( in radial and/or axial direction) is arising during transit of the ion beam through the ion optical system, where parts of the ion beam may be cut-off at beam-defining stops.
The well known "Exponential Law" correction formula is:
(a)
The discrimination factors sU and sN are mass dependent values near to "1", their mass dependence may be assumed to be approximately linear, i.e.
sU = 1 ± S *DmU and sN = 1 ± S * DmN,
DmU = m2 - m1 or DmN = m4 - m3 being the mass differences of the unknown and the known ratio, respectively.
S is the static "mass discrimination per mass unit".
How do we know the static mass discrimination factor, or, in other words, how can we seperate static and dynamic (evaporation induced) discriminations?
We know from Langmuir"s evaporation law that the observed
sU = 1 ± S *DmU and sN = 1 ± S * DmN,
DmU = m2 - m1 or DmN = m4 - m3 being the mass differences of the unknown and the known ratio, respectively.
S is the static "mass discrimination per mass unit".
How do we know the static mass discrimination factor, or, in other words, how can we seperate static and dynamic (evaporation induced) discriminations?
We know from Langmuir"s evaporation law that the observed
Unfortunately, we have available the biased RUobs resp. rNobs values only, and we, hence, will obtain a biased "observed" true ratio RUobs , if we use the observed isotope ratios for fractionation correction.
RUobs is different from the "evaporation-bias-free" true ratio (RU):
RUobs is different from the "evaporation-bias-free" true ratio (RU):
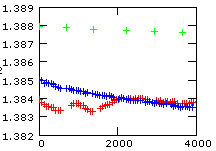
The figure on the left shows a plot of the 144/146Nd raw ratio (rN) for the first hour of our high precision runs. Ideal fractionation would require a starting raw ratio of
Remark: Species-dependent mass effects would modify the 143/144values by ± 5 to 10 ppm.
In the light of such results it seems to be neccessary to have a much better knowledge of the real "true" isotope ratios of standard samples. This alone would enable us to assess observed non-evaporation-induced biases, which apparently do have much influence on the normalised isotope ratio. If we, just as an example, would use the "Caltech Standard" value instead of the LaJolla value, the observed static biases would appear to be a lot smaller and, thus, would have much less influence on the assessment of possible normalisation errors.
There is no doubt: If the above assumptions on static discriminations are correct, statically biased raw ratios result in fractionation corrected "true" ratios, whose differences to corrected, but unbiased values are outside the error limits of modern high precision runs. Hence, they are significant, although their absolute size, unfortunately, may be completely unknown.
And, they may, e.g., give rise to speculate on the necessity of empiric "second order corrections".
In any case, it seems to be wise to check static discriminations of two instruments, before their high precision results are seriously compared.
In the light of such results it seems to be neccessary to have a much better knowledge of the real "true" isotope ratios of standard samples. This alone would enable us to assess observed non-evaporation-induced biases, which apparently do have much influence on the normalised isotope ratio. If we, just as an example, would use the "Caltech Standard" value instead of the LaJolla value, the observed static biases would appear to be a lot smaller and, thus, would have much less influence on the assessment of possible normalisation errors.
There is no doubt: If the above assumptions on static discriminations are correct, statically biased raw ratios result in fractionation corrected "true" ratios, whose differences to corrected, but unbiased values are outside the error limits of modern high precision runs. Hence, they are significant, although their absolute size, unfortunately, may be completely unknown.
And, they may, e.g., give rise to speculate on the necessity of empiric "second order corrections".
In any case, it seems to be wise to check static discriminations of two instruments, before their high precision results are seriously compared.
Apparently, we need quite some assumptions for the correct assessment of any static
discriminations, if they should exist at all. In particular, we presuppose that fractionation ideally
follows our theoretical expectations.
i.e.: The light isotope is enriched in the vapor phase.
We now use the very first raw (observed) isotope ratio r (0)obs of the known (normalising) ratio of a run and we then assume that only a minor amount of sample has been evaporated at the time when we acquire these first ion currents.
Therefore, for the beginning of the run, we may assume Rbulk@Rtrue = RN
If the measured first ratios of a run are different from this expectation, we can assume that this difference may be possibly attributed to a static discrimination S, hence
We now use the very first raw (observed) isotope ratio r (0)obs of the known (normalising) ratio of a run and we then assume that only a minor amount of sample has been evaporated at the time when we acquire these first ion currents.
Therefore, for the beginning of the run, we may assume Rbulk@Rtrue = RN
If the measured first ratios of a run are different from this expectation, we can assume that this difference may be possibly attributed to a static discrimination S, hence
isotope ratio is given by
(RN ~> LaJolla Standard , assuming evaporation of Nd atoms)
Computation of
RUobs / Ru
RUobs / Ru
| rU, rN | isotope ratios in the vapor above the evaporating surface, which are changing with time by progressive evaporation, depending on their masses, |
| rUobs, rNobs | ratios of the ion currents in the ion collectors, which may be additionally biased by constant discrimination factors σU resp.σN, i.e.: |
| rUobs = σU * rU resp. rNobs = σN * rN. | |
| RU, RN | "true" isotope ratios of the sample, |
| m1, m2 | masses of the unknown ratio, (m1 > m2) |
| m3, m4 | masses of the known ratio, (m3 > m4) |
or
with m2 > m1 and
,
(b)
All three runs show, as compared to the total amount of fractionation, significantly smaller starting values and we state, in a first approximation, that they might be additionally biased by static discriminations. One run (red track), in particular, even shows reverse fractionation sections within the first halve hour, before it seems to continue to fractionate in a similar way as its related run (blue). However, there exists another extended period of reverse fractionation later in this run (see the preceding chapter Theory in a real world). In fact, this run fractionates only more then 2 hours from the beginning of the evaporation in such a way as we would (naively) expect.
On the other side, the blue run fractionates relatively fast during the first hour and it shows vittually no fractionation for the following 5 1/2 hours.
Such, and similar, effects are observed quite often, in particular at the beginning of a run: Regular fractionation (whatever that is) apparently needs some time until the evaporation process may have reached a kind of equilibrium state.
As a matter of fact, we don't really know, whether our samples evaporate as atoms or as molecules ( e.g. as oxyde, NdO resp. Nd2O3 ), or as a mixture of both. And we may also expect that the ratio of atomic and molecular species, which evaporate, will not stay constant during a run. Such an assumption would, by the way, contribute to explain reverse fractionation.
On the other side, possible species-dependent mass effects are at least two times smaller than the differences between the green and the red/blue runs.
Out of this reason, we tend to attribute the same size of static discriminations to both, the blue and the red run, whilst the green run (probably) shows a significantly smaller static bias.
With all these assumptions in mind, we now compute the static biases of the runs by using equ.(b) above:
With b=1.00692, we obtain
For the "green run": r(0)obs=1.388, and hence S ~ 0.0025 per mass unit.
For the "blue" and the "red run": r(0)obs=1.385, and hence S ~ 0.0035 per mass unit.
With these numbers, and by using equ. (a) above, we may easily assess the deviation of the fractionation corrected ratios from the "true" ratio, if raw ratios are statically biased:
We get:
On the other side, the blue run fractionates relatively fast during the first hour and it shows vittually no fractionation for the following 5 1/2 hours.
Such, and similar, effects are observed quite often, in particular at the beginning of a run: Regular fractionation (whatever that is) apparently needs some time until the evaporation process may have reached a kind of equilibrium state.
As a matter of fact, we don't really know, whether our samples evaporate as atoms or as molecules ( e.g. as oxyde, NdO resp. Nd2O3 ), or as a mixture of both. And we may also expect that the ratio of atomic and molecular species, which evaporate, will not stay constant during a run. Such an assumption would, by the way, contribute to explain reverse fractionation.
On the other side, possible species-dependent mass effects are at least two times smaller than the differences between the green and the red/blue runs.
Out of this reason, we tend to attribute the same size of static discriminations to both, the blue and the red run, whilst the green run (probably) shows a significantly smaller static bias.
With all these assumptions in mind, we now compute the static biases of the runs by using equ.(b) above:
With b=1.00692, we obtain
For the "green run": r(0)obs=1.388, and hence S ~ 0.0025 per mass unit.
For the "blue" and the "red run": r(0)obs=1.385, and hence S ~ 0.0035 per mass unit.
With these numbers, and by using equ. (a) above, we may easily assess the deviation of the fractionation corrected ratios from the "true" ratio, if raw ratios are statically biased:
We get:
Unknown Ratio
143/144Nd
144/150Nd
Green run
1.000 023
( +23 ppm )
0.999872
( -130 ppm )
Blue run
1.000 030
( +30 ppm )
0.999862
( -140 ppm )
Whilest evaporation induced discriminations systematically depend on mass and on time (in fact, they depend on the fraction of evaporated sample at a given time), static discriminations are virtually constant during a measurement, but they oftenly also are mass dependent.
The question is, wether such static discriminations can be corrected similarly, and at the same time, as the evaporation induced discriminations by the application of one of the common fractionation laws, albeit their origin is for sure not evaporation induced.
I will try to find the answer with the "Exponential Law" as an example, using the raw data of three high precision runs as mentioned in section "Theory in a real world".
We are using the following annotation for the correction of an "unknown" ratio (subscript U) by means of the application of a "known" ratio (subscript N).
The question is, wether such static discriminations can be corrected similarly, and at the same time, as the evaporation induced discriminations by the application of one of the common fractionation laws, albeit their origin is for sure not evaporation induced.
I will try to find the answer with the "Exponential Law" as an example, using the raw data of three high precision runs as mentioned in section "Theory in a real world".
We are using the following annotation for the correction of an "unknown" ratio (subscript U) by means of the application of a "known" ratio (subscript N).
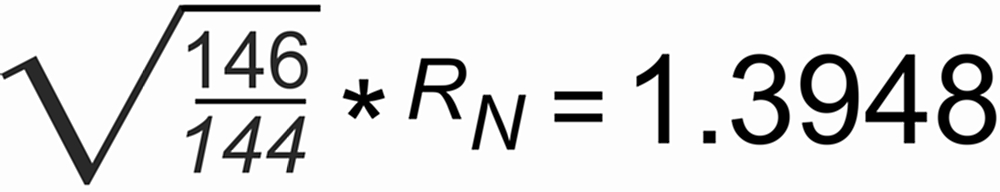
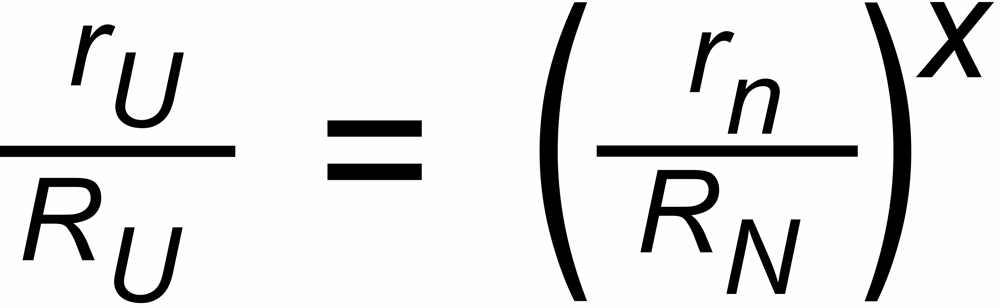
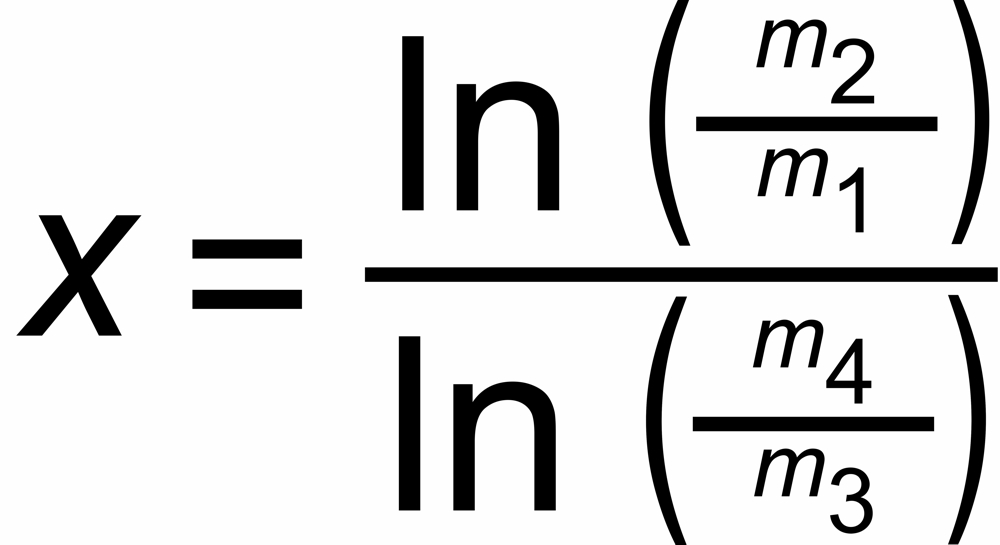
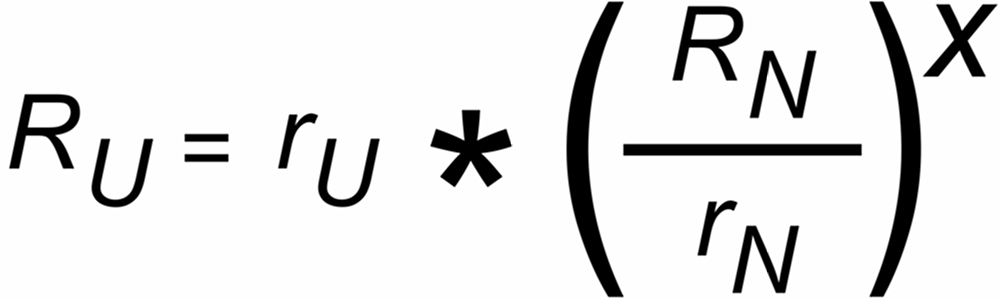
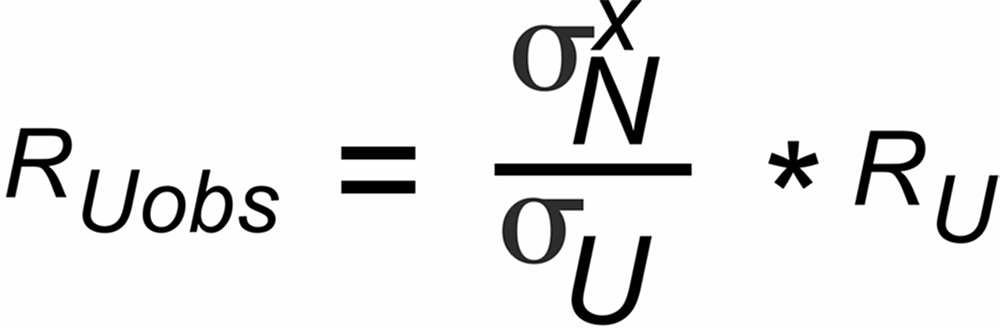
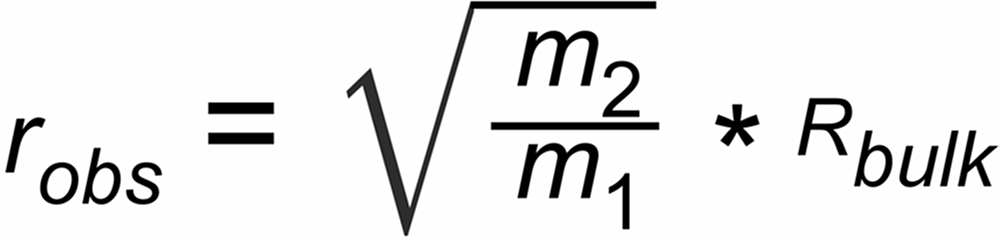
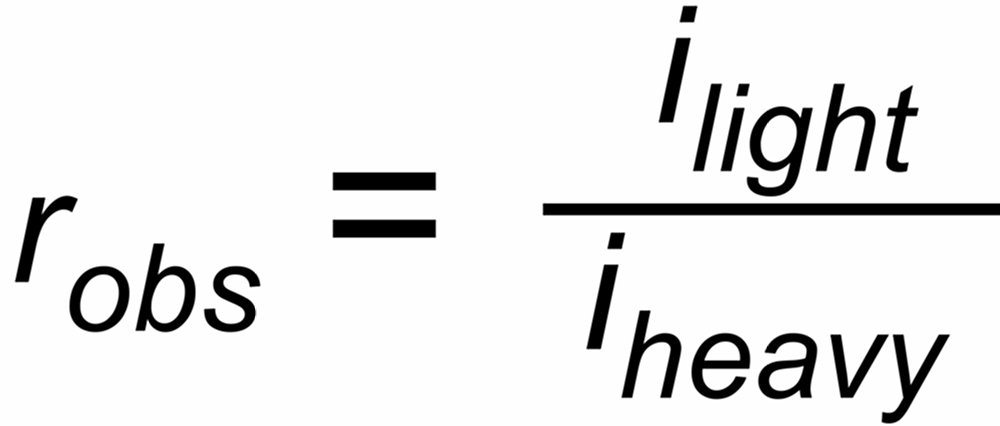
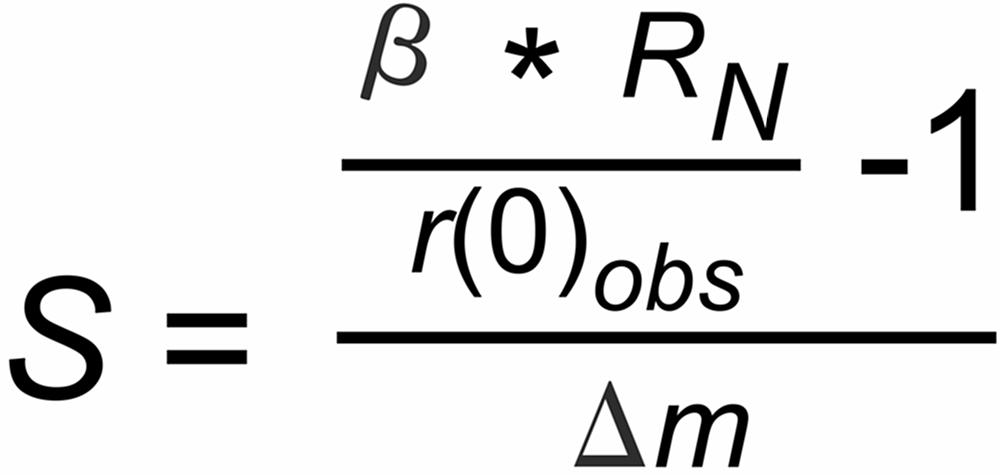

Dr. Karleugen Habfast: Theory of Fractionation Correction - Auto Correction of static discriminations







