
Besides the causal Rayleigh law , also other, empirically defined "fractionation laws" are in use. All these laws are based on the assumption that fractionation is governed by a suitable "fractionation coefficient q" , which relates the masses of the two species of the fractionated ratio in some way to the observed ratio.
The Exponential law is based on the assumption that fractionation is governed by the following simple relation:urce, the ion current 'i' reflects the rate of flow (dn/dt) of those particals which hit the hot surface.
The Exponential law is based on the assumption that fractionation is governed by the following simple relation:urce, the ion current 'i' reflects the rate of flow (dn/dt) of those particals which hit the hot surface.
The resulting correction formula is:
Empirically one best chooses
The Rayleigh law and the Exponential law have slightly curved fractionation lines.
A Linearized Rayleigh law can be derived from the above Rayleigh fractionation equation:
Their average slope is
The graphs of the other fractionation laws are straight lines with slope X as given above.
q is a (time dependent) number << 1.
The resulting correction formula is:
The resulting correction formula is:
q is assumed to only depend on time (i.e., not on mass), and it is assumed that it is the same for all ratios. Hence it may be eliminated. The resulting correction formula is:
It can be shown that the Exponential law is a very good approximation of the Rayleigh law.
The power law assumes the following relation between the ratio and its masses:
The power law assumes the following relation between the ratio and its masses:
The Linear law is even simplier. It is mainly based on earlier or 'historic' observations (see footnote 5):
and the resulting correction formula is
.

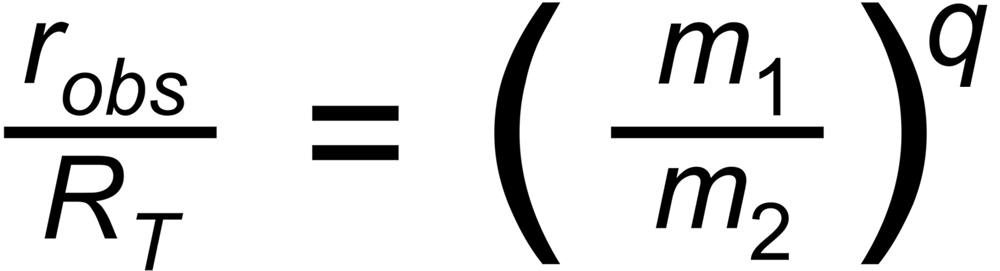
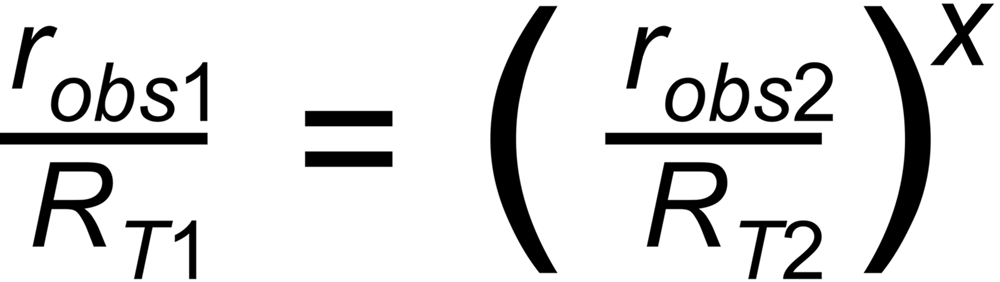
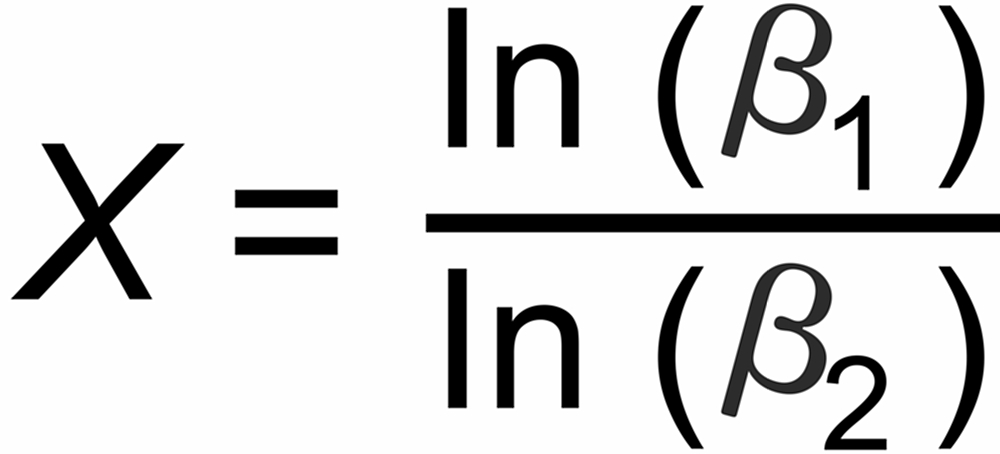
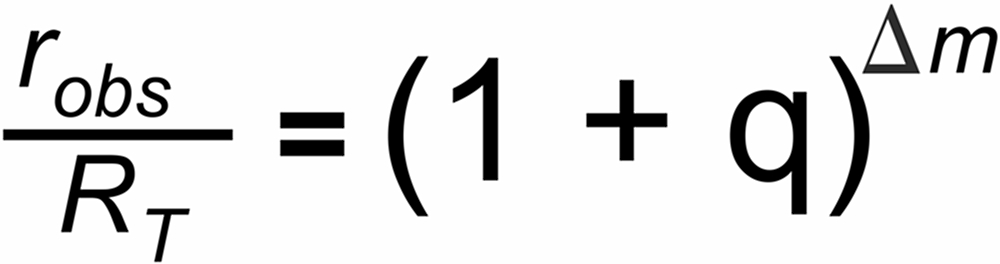
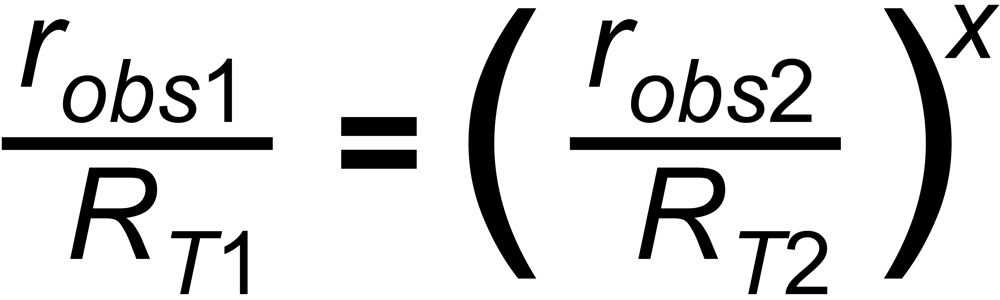
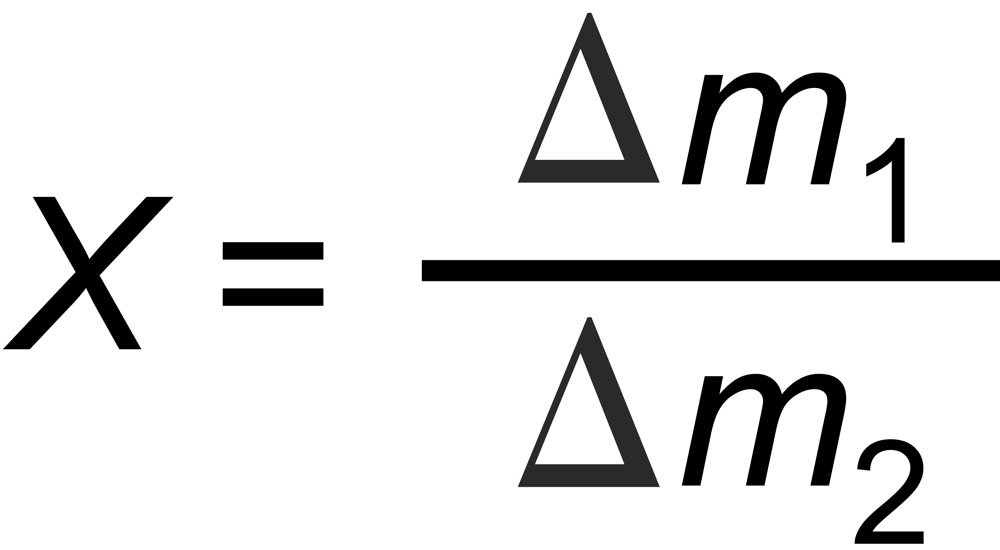
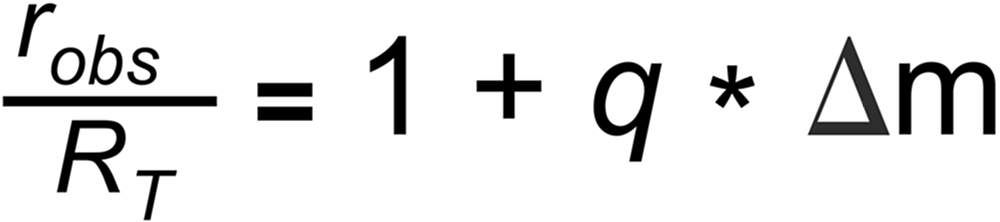
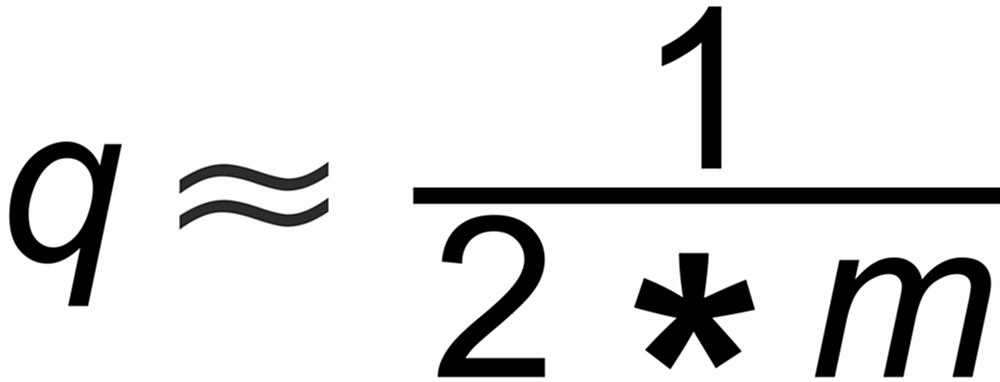
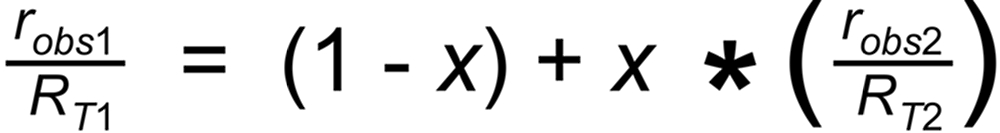
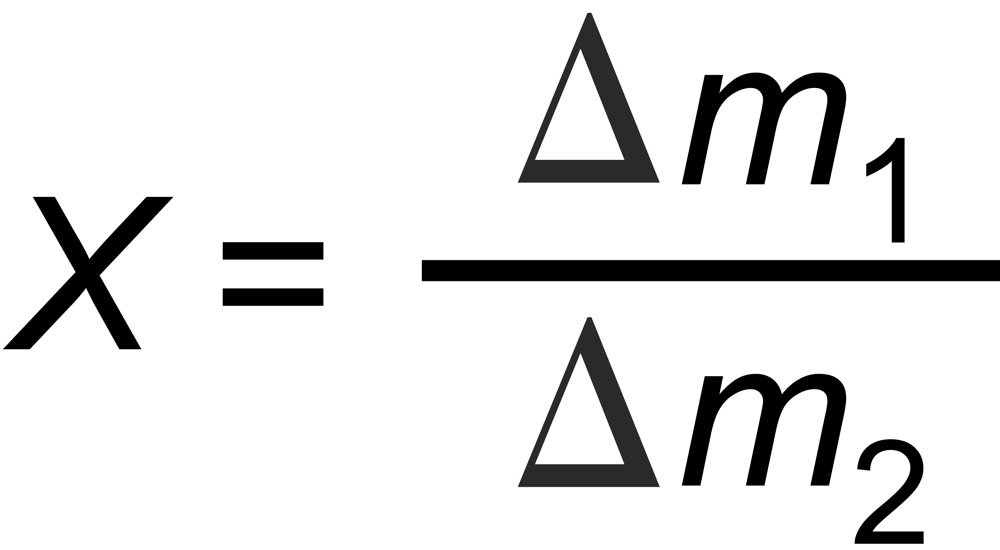
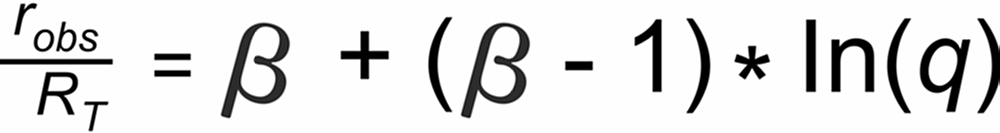

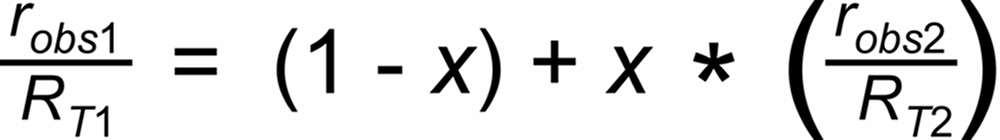
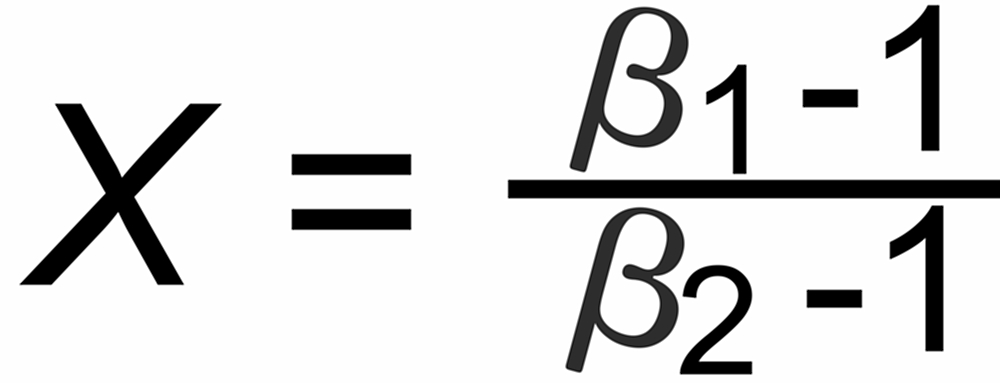
Dr. Karleugen Habfast: Theory of Fractionation Correction - Empiric Laws







