
Let r1 be the "unknown" and r2 the "known" ratio (i.e. the ratio whose "true" ratio RT2 is known), then, resolving the above "laws" for RT1 allows the computation of the "true" ratio of r1.
This computation is applied to each individual pair of ratios, as calculated from the raw data set of the data file (after all required intensity corrections have been applied).
The formula for the Rayleigh law cannot be given explicitly (see footnote 6):
The general formula for the "Exponential like" laws (Exponential & Power ) look like this (U: unknown, N: known ratio):
This computation is applied to each individual pair of ratios, as calculated from the raw data set of the data file (after all required intensity corrections have been applied).
The formula for the Rayleigh law cannot be given explicitly (see footnote 6):
The general formula for the "Exponential like" laws (Exponential & Power ) look like this (U: unknown, N: known ratio):
X as given above for the individual laws, e.g.
for the "dual collector dual jump Sr" scheme, and
These "computed" observed ratios of the known (normalizing) ratio are inserted into the above formulae (and are also used for the Rayleigh law iteration). This procedure, however, places constraints on the choice of the masses and on the kind to define the ratios:
a) The "middle" mass of both ratios must be identical for both ratios, and
b) both ratios must be defined "in the same direction", i.e. either low mass/high mass or vica versa. Corresponding to this, the "true" value for the “known" ratio must be choosen.
Just for curiosity, we give the dual collector Sr formula:
a) The "middle" mass of both ratios must be identical for both ratios, and
b) both ratios must be defined "in the same direction", i.e. either low mass/high mass or vica versa. Corresponding to this, the "true" value for the “known" ratio must be choosen.
Just for curiosity, we give the dual collector Sr formula:
The given algorithms can be directly applied to any pair of ratios, one being the "unknown" and the other the "known" or normalizing ratio. There is no restriction for the choice of the masses of the three or four selected ion beams, and you are free to define the ratios as you like.
For the dual collector dynamic data acquisition schemes one or two auxilliary ratios (raux) are measured besides the "unknown" ratio, whilst the known ratio is not directly measured.
However, these schemes are designed in such a way, that the "observed known ratio" can be easily calculated:
For the dual collector dynamic data acquisition schemes one or two auxilliary ratios (raux) are measured besides the "unknown" ratio, whilst the known ratio is not directly measured.
However, these schemes are designed in such a way, that the "observed known ratio" can be easily calculated:
This resolves to
The formula for the "Linear like" laws is:
for the Exponential law
for the Linearized Rayleigh law.
With X as given above for the individal laws, e.g.
for the "dual collector triple jump Nd" scheme.
For the power and the linear law, we have
and the final formula, thus, results in the well known (historic) form:

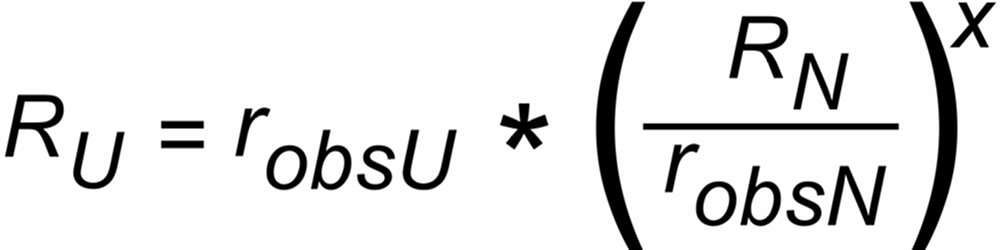
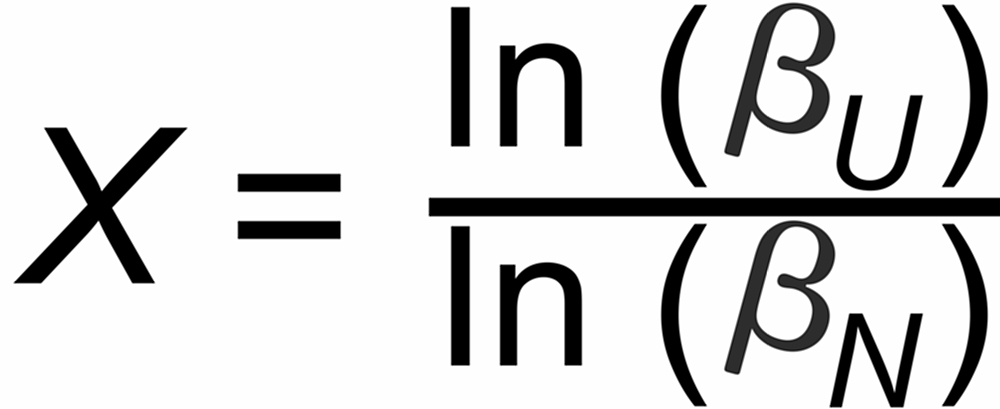
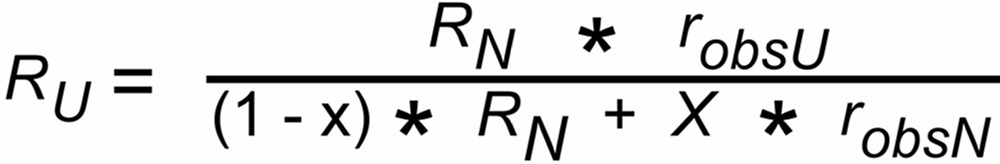
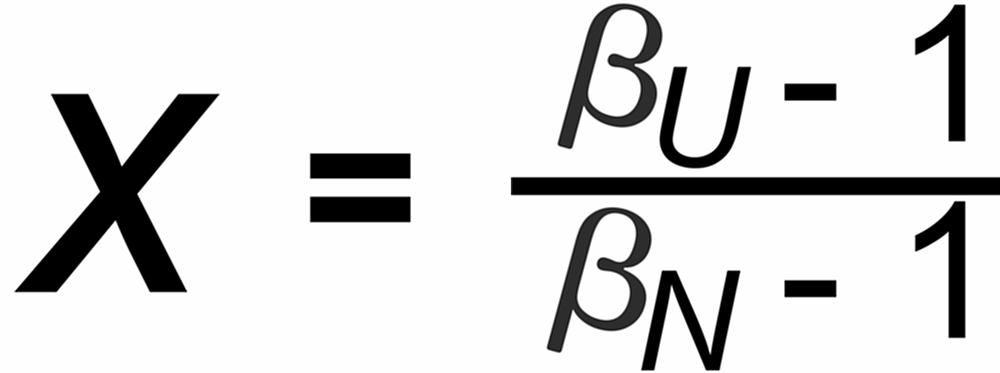


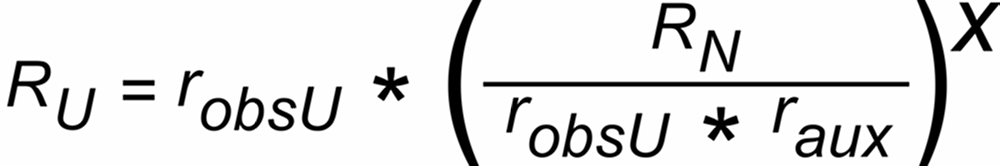
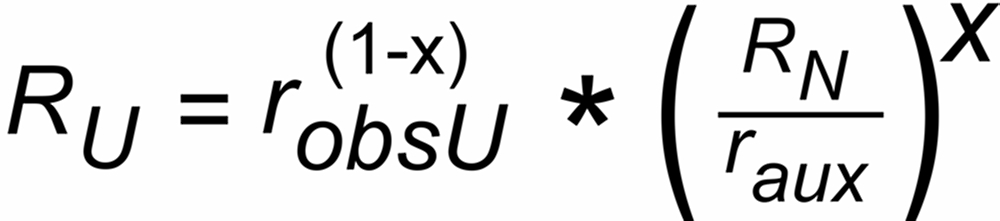
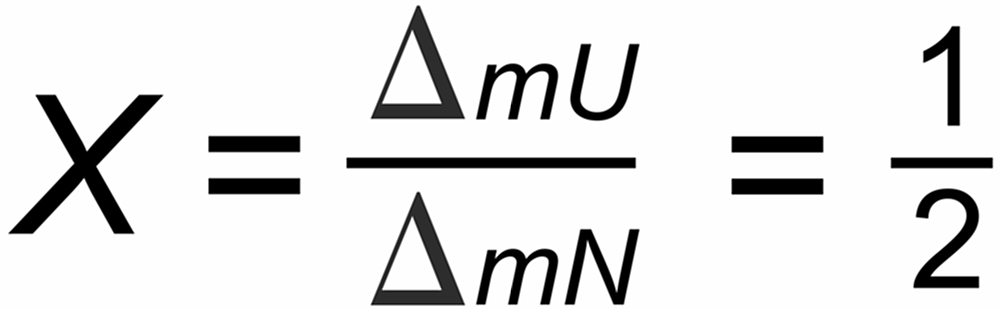
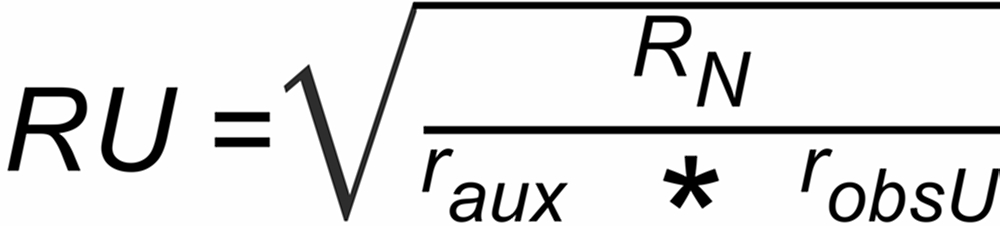
Dr. Karleugen Habfast: Theory of Fractionation Correction - Fractionation Correction Formulae







